题目描述

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回  -1。

示例 1: 输入: haystack = “hello”, needle = “ll” 输出: 2

示例 2: 输入: haystack = “aaaaa”, needle = “bba” 输出: -1

说明: 当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。 对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。

算法原理

KMP的经典思想就是:当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免从头再去做匹配。

我们现在的问题是 在文本串中找到与模式串匹配的子串。待匹配的串称为文本串，做匹配的串称为模式串。

设文本串长m,模式串长n，显然暴力匹配时间复杂度为O(mn)。

问题在于每次匹配失败我都从文本串的下一个字母和模式串的第一个字母开始重新匹配，如果我能利用一些已经匹配的信息，这样就可以省去很多无用的操作。

进一步了解这个算法之前我们要先了解一下前缀和后缀。

  • 前缀：包含字符串首位，不包含尾位的子串。
  • 后缀：包含字符串尾位，不包含首位的子串。

KMP算法的核心就是找到匹配失败的前一个用来匹配的模式串子串的最长公共前后缀长度。

注意上面这段话不仅仅是在进行模式匹配的时候体现，在求前缀表的时候也有体现！

思路解析

求前缀表

刚看完原理视频的时候觉得原理并不难理解，确实如此，如果考试让我写前缀表的话我可以很快地写出来，但是怎么在代码中高效实现求所有子串的前缀表呢？把所有前缀和后缀都写出来比较吗？笨方法，双指针法可以提高算法的效率。

设计双指针的原则是 一个遍历指针，另一个指向最长相等前缀。通过后面这个指针就可以知道当前子串的最长相等前后缀长度了。

首先初始化双指针和next数组。遍历指针i以及前缀指针j，next数组的长度和模式串长度相等。前缀指针j的值就是位置0 - i（包含i）的子串的最长公共前后缀长度。最开始只有一个字符，故初始化为0，next[0] = 0。所以我们从i = 1开始遍历。

1
2
3
4
5
int j = 0;
next[j] = 0;
for (int i = 1; i < s.length(); i++){
	...
}

我们需要处理两类情况。

  1. i与j位置字符不匹配。
  2. i与j位置字符匹配。

直观的思想是：如果匹配，那么意味着找到相等的前后缀字符了，长度加一，j + 1.
如果不匹配，我就需要减小j直到字符匹配或者j减小到0都不匹配，next表项直接填0。

直接一个个减j嘛？笨方法，和暴力解法没有区别，只是把暴力挪到了求前缀表的操作上。那应该怎么办呢？

答案就是： 利用已经求出来的前缀表！

这里我需要借用大佬博主的博客可视化地呈现情况。

匹配的情况是这样的。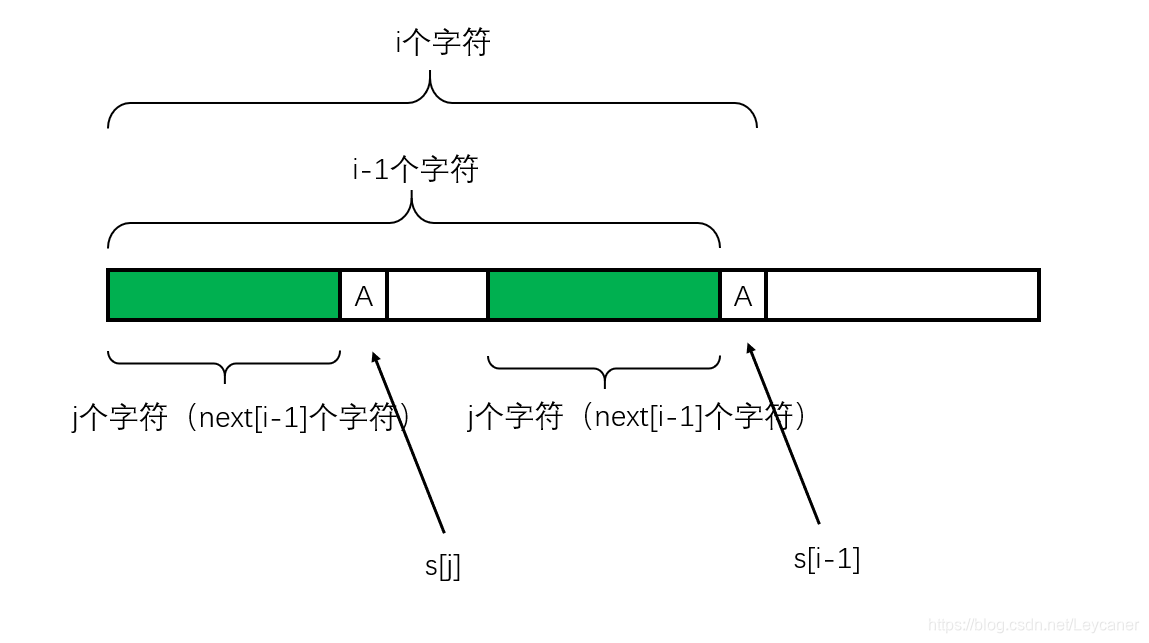
img/KMP1.png
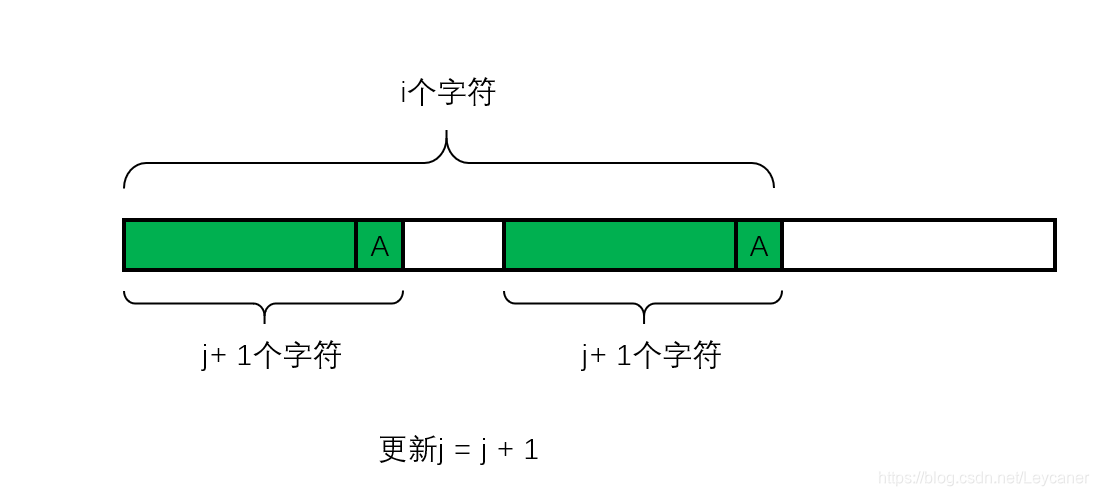
img/KMP2.png

如果遇到不匹配的情况如下：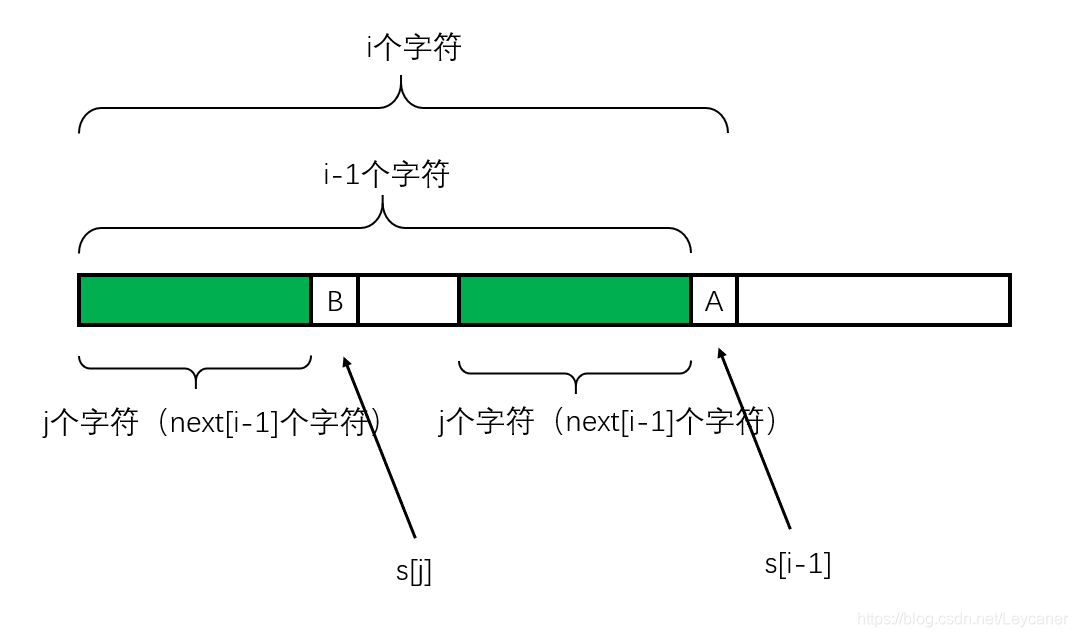
img/KMP3.png
显然深绿色的部分不能用了。我得在左边深绿色的部分中找到一个前缀，和以A作为结尾的后缀进行匹配。对应于下图（注意下图是以B作为结尾的后缀)就是大括号里的内容对应进行匹配。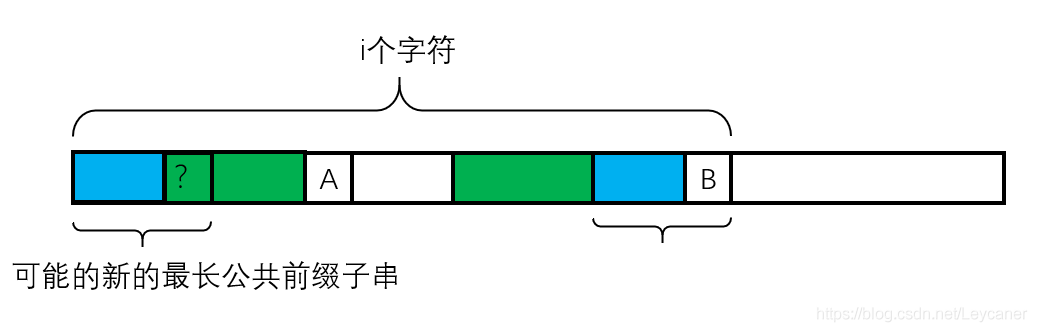
img/KMP4.png

换句话说，我需要在深绿色的部分中找到两个子区间，其中左边的子区间从模式子串最左边开始延伸，右边的子区间从模式子串B之前开始延伸。我需要找到最大长度的这两个子区间，来考察左区间加上？字符，右区间加上B是否匹配（其实也就是判断？是否等于B）这样就能够最大程度地利用已经进行过匹配的字符串。

通过上面的分析，其实已经可以知道：蓝色区间就是深绿色部分的最长公共前后缀！ j要回退到的地方就是图中？的地方！对应于代码，就是A的上一个字符的next数组值！就是next[j-1]! 要进行的操作就是 j = next[j-1]!

神奇的操作，恕我见识有限，不知道这种像最优子结构但好像也不是的操作叫什么名字。和KMP的算法思想对应，我觉得可以认为：在拿深绿色部分 + A的子串作为模式串（因为我们有A之前的next表），深绿色部分 + B的子串作为文本串。当A和B不匹配时，就退回到？的地方。这就是KMP思想的体现！

个人觉得最难的地方已经讲完了，剩下的就只需要考虑一些逻辑条件和边界条件即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vector<int> getNextTable(const string& s){
        vector<int> next(s.length());
        int j = 0;
        next[j] = 0;
        for (int i = 1; i < s.length(); i++){
            while (j > 0 && s[i] != s[j]){
                j = next[j-1];  // 前缀回退,如果j本来就是0那没必要退，因为退无可退
            }
            if (s[i]==s[j]){
                j++; 
            }
            next[i] = j;
        }
        return next;
    }

模式串匹配

在匹配的时候需要考虑三种情况。

  1. 对应字符匹配
  2. 对应字符不匹配，模式串指针指向0
  3. 对应字符不匹配，模式串指针不指向0

匹配就两者步进即可；不匹配，若是模式串指针指向0，就代表没有可以利用的匹配信息，文本串指针加一即可。若是不指向0，就代表有可以利用的信息，指针回退到next[指针位置 - 1]的值对应的位置即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector<int> next = getNextTable(needle);
        int ph=0,pn=0;
        while(ph < haystack.length() && pn != needle.length()){
            // successfully match
            if (haystack[ph]==needle[pn]){
                ph++,pn++;
            }
            else if (pn != 0){ // pn = 0就退无可退了
                // match fail
                pn = next[pn-1];
            }
            else{ // 如果pn=0并且匹配不上，那么没有可以利用的已经匹配的信息，直接从haystack的下一个位置匹配即可
                ph++;
            }
        }
        if (pn == needle.length())  return ph - pn;
        return -1;

最后当模式串指针pn遍历完毕之后，ph - pn就是第一个匹配字符的下标。如果pn没有遍历完而是ph遍历完了，那代表文本串和模式串不匹配，输出-1。

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
vector<int> getNextTable(const string& s){
        vector<int> next(s.length());
        int j = 0;
        next[j] = 0;
        for (int i = 1; i < s.length(); i++){
            while (j > 0 && s[i] != s[j]){
                j = next[j-1];  // 前缀回退,如果j本来就是0那没必要退，因为退无可退，那为什么不逐一退呢？为什么要退到nextTable
            }
            if (s[i]==s[j]){
                j++; 
            }
            next[i] = j;
        }
        return next;
    }

    int strStr(string haystack, string needle) {
        vector<int> next = getNextTable(needle);
        int ph=0,pn=0;
        while(ph < haystack.length() && pn != needle.length()){
            // successfully match
            if (haystack[ph]==needle[pn]){
                ph++,pn++;
            }
            else if (pn != 0){ // pn = 0就退无可退了
                // match fail
                pn = next[pn-1];
            }
            else{ // 如果pn=0并且匹配不上，那么没有可以利用的已经匹配的信息，直接从haystack的下一个位置匹配即可
                ph++;
            }
        }
        if (pn == needle.length())  return ph - pn;
        return -1;
    }

来源