CNN学习笔记
参考资料
可视化网站:https://poloclub.github.io/cnn-explainer/#article-input
卷积&全连接&卷积模式:https://zhuanlan.zhihu.com/p/76606892
自从我转专业到软件以来,卷积神经网络这个词就一直萦绕在我耳边,CNN的大名也是无数次地听到。但即使如此,对于什么是卷积,对于卷积神经网络训练的过程,我从来没有真正掌握,今天在选修课上又一次接触到了这一概念,想到之后保研面试肯定是要问这些的,不如现在就趁着时间还早打好基础,把机器学习的系统思维真正地构建起来,为之后的保研和陶瓷做准备。

1 卷积
“卷积”一词来源于信号处理领域,人们想要知道一个输入信号在经过一个可以用单位冲击响应函数
假设有输入信号
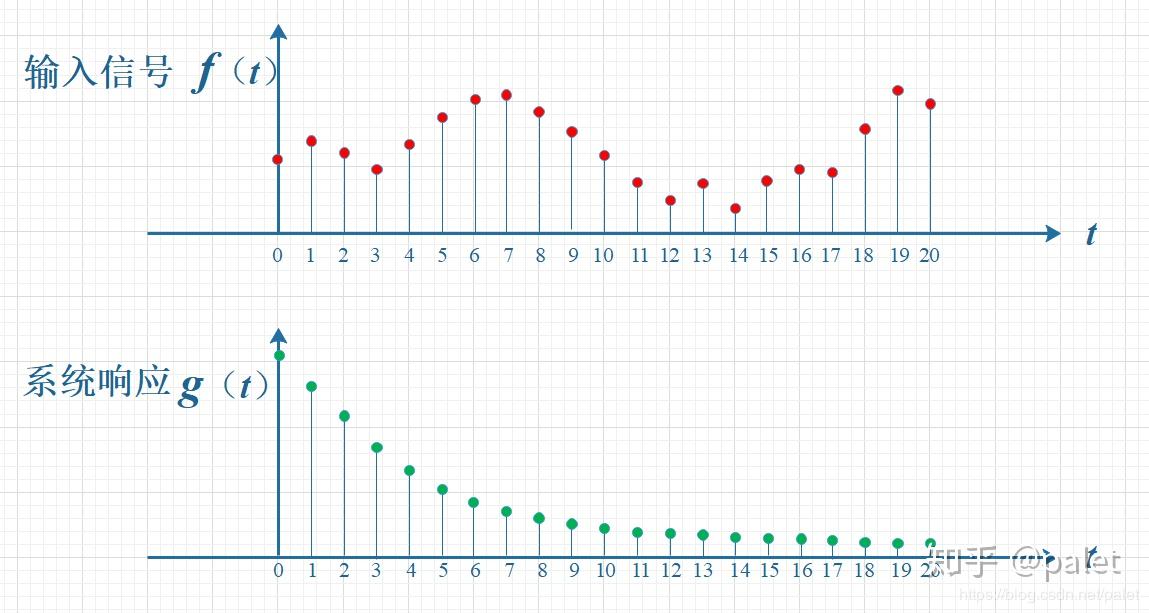
首先要知道,某一时刻的信号输出值是当前和之前所有输入信号的累积效果,我现在想知道
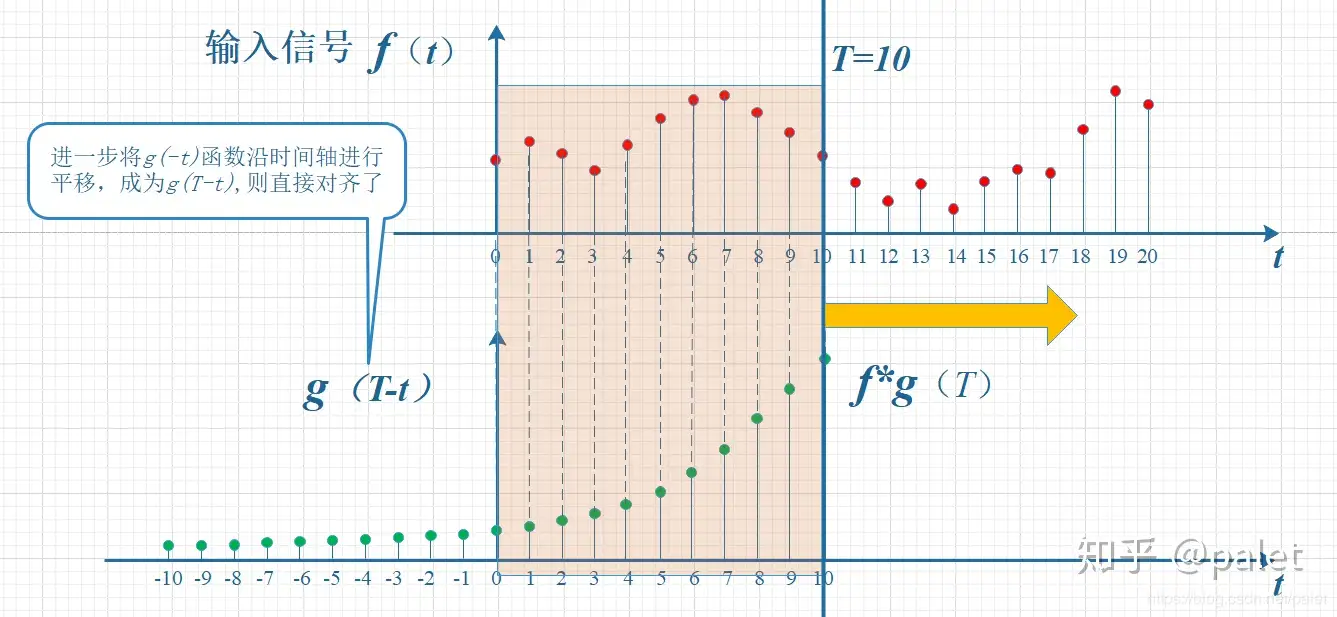
由此可推导出连续函数的卷积公式:
离散型随机变量也可以进行卷积,只要把上面的积分换成求和即可,但是在那之前,我们先从概率论的角度推一遍卷积公式。
条件非常简单,求两个独立随机变量X、Y的和Z = X + Y的概率密度函数。

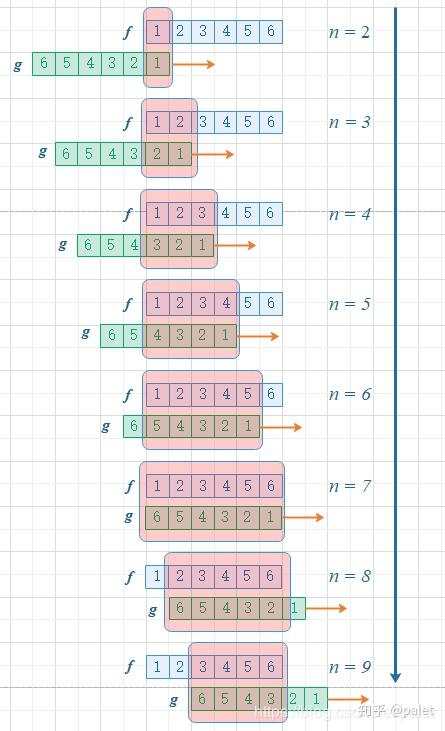
我们再来看看离散型随机变量的例子,我们以掷骰子为例,由前面的证明我们知道,我们需要构造的是两次掷的骰子点数之和。
假设我们要求
。对应在图像上就是先把第二个骰子“卷”过来再对应位置相加相乘。
CNN中所用的是多维互相关,也就是没有翻转的卷积。我们先来看多维卷积,具体来说是二维,公式如下:
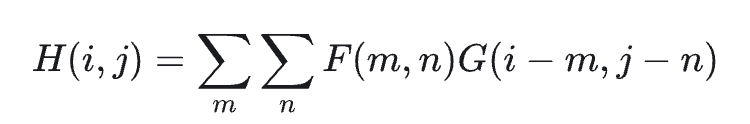
该操作需要先将卷积核翻转,然后再与输入点相乘。但是CNN中省略了翻转这一过程,因为翻转本身没有什么意义,还会改变特征的方向特征,所以CNN中用的是互相关(Cross-Correlation):
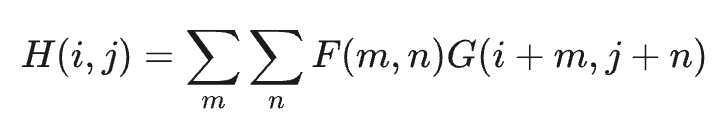
另外,卷积操作其实就是对输入向量乘以一个稀疏的全连接矩阵。
卷积和全连接实质上都是一组线性转换,但是卷积相比全连接而言,其参数矩阵更加稀疏,kernel matrix 中很多为零(sparse connectivity),同时非零部分的参数实际上是共享的(parameter sharing)。这两个特点让卷积可以大大减少参数的数量,同时同一套参数(卷积核)在多个地方复用更有利于捕捉局部的特征。
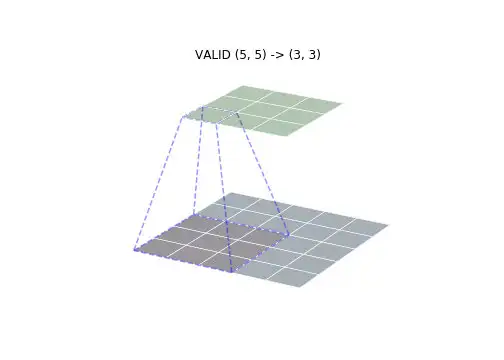
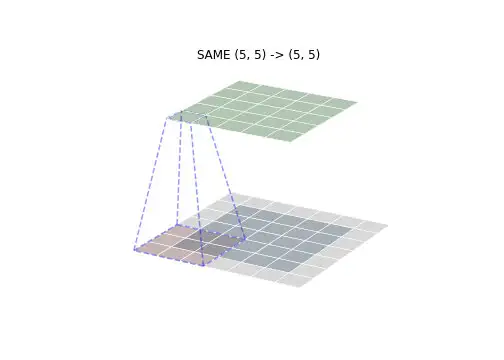
卷积有三种模式,分别是FULL,VALID和SAME模式。下面的图像可以直观表述它们的区别:
- FULL: - - 从有相交的地方开始卷积,该方法输出的尺寸最大
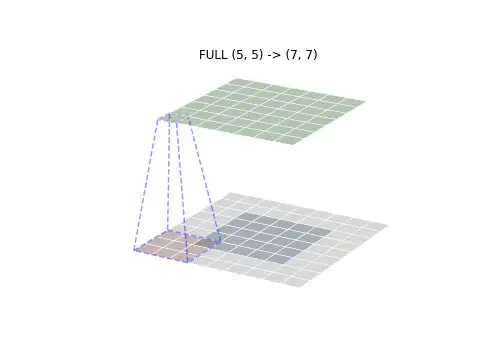
- VALID - - 从重叠的地方开始卷积,参考网站用的就是这种方法
- SAME – 输出大小 = 输入大小,可能需要不对称Padding
2 CNN基本概念
CNN首先是一个神经网络,是一种用来在数据中识别模式的算法。神经网络是由一系列组织成层的有着Weights和Bias参数的神经元构成的。
- tensor张量,表示多维数组,0维张量就是数字,1维张量就是向量,2维张量就是矩阵,n维张量就是n维矩阵。
- Neuron神经元是一个接受多个输入,提供一个输出的计算单元
- Layer层是一系列执行相同类型操作的神经元的集合,它们有相同的超参数(P,KS,S)
- Weights&Bias权重与偏置是每一个神经元在训练的时候优化的参数。
3 CNN层
3.1 Input Layer输入层
由于CNN一般被用来处理图片分类问题,所以一般输入图片有RGB三个通道。
3.2 Convolutional Layer卷积层
这是CNN的核心层,重要的是分清楚两层之间的联系。注意到下图中的卷积层是全连接的,也就是说每一个卷积层神经元都连接着上一个层的所有神经元,用含有相同超参数,但是具体weight不同的卷积核对三个通道分别进行卷积后再将对应位置的值相加,最后加上偏置向量Bias就完成了一个神经元的计算。
需要注意的是,如果按照这种全连接的方式,在input和conv层之间就需要3 * 10 = 30个有着不同weights的卷积核。
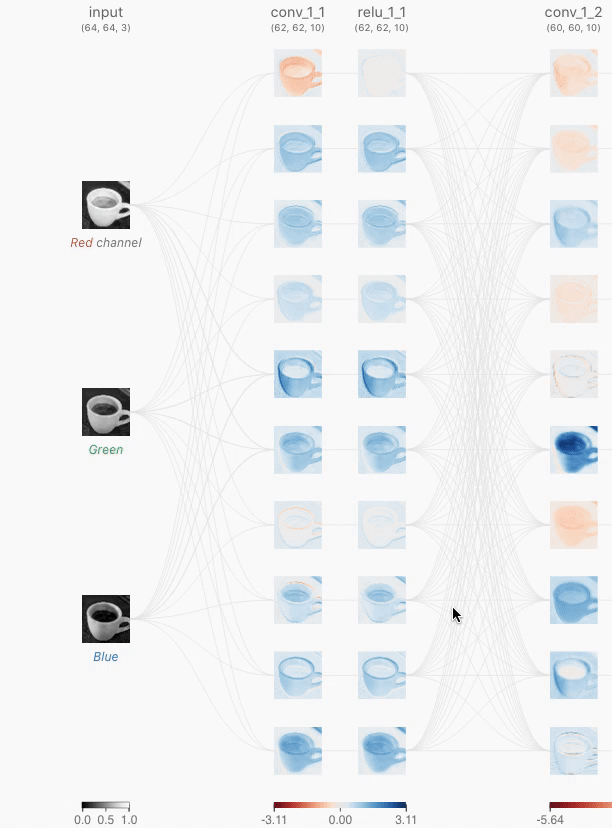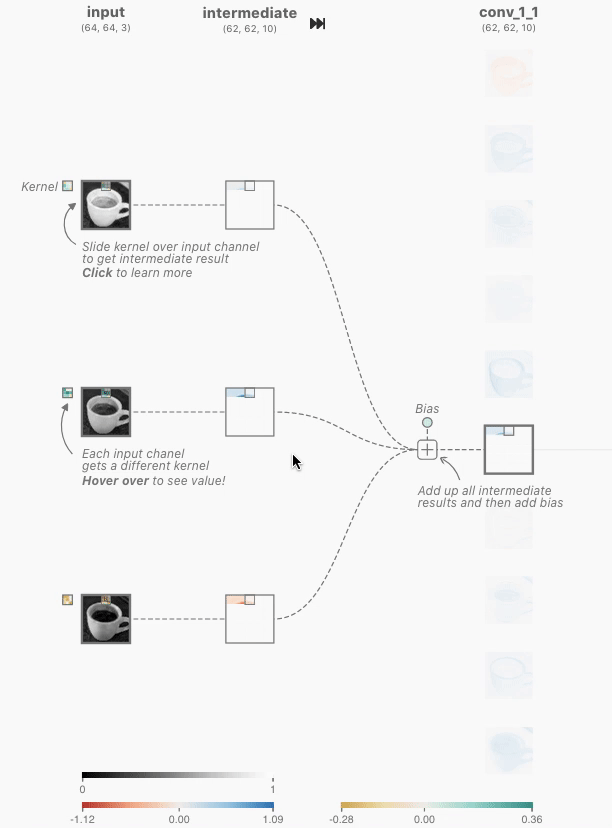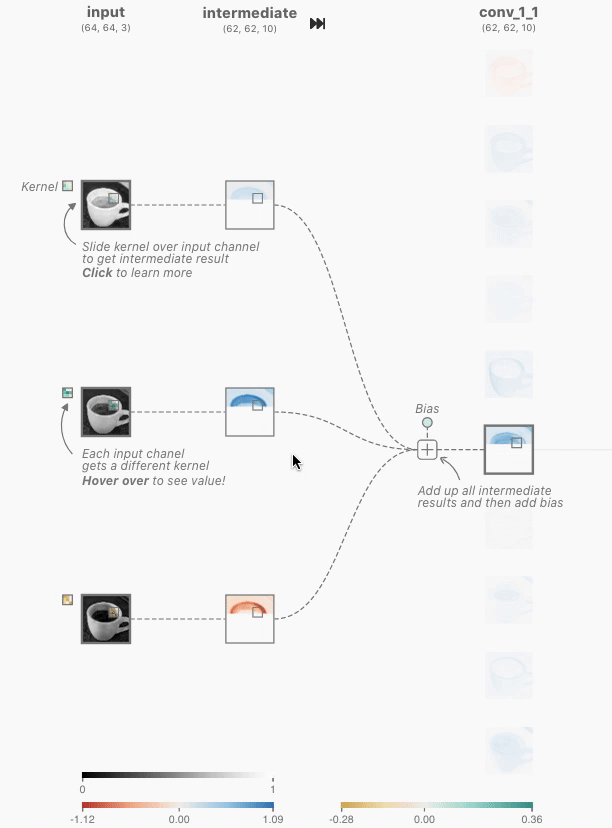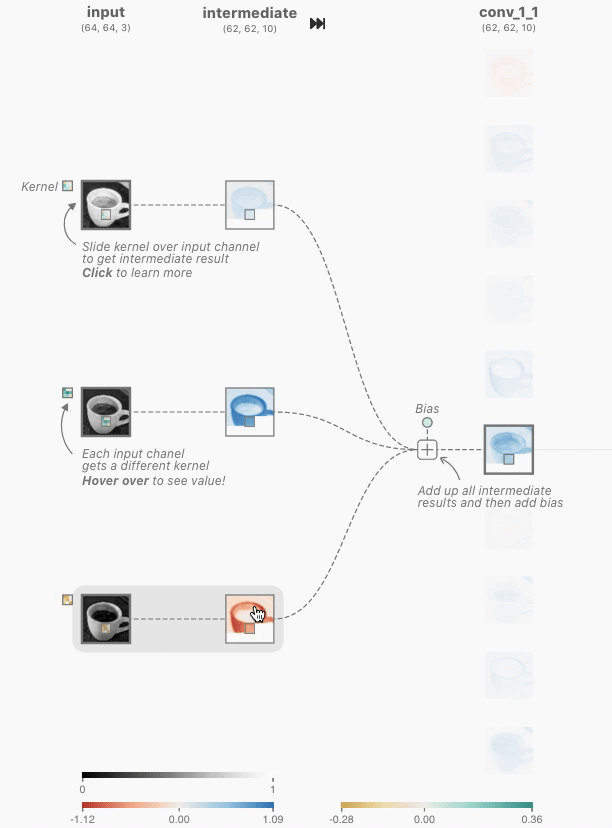
3.3 Pooling Layer池化层
池化层的目的是减小网络规模,降低计算量和计算成本。
其中用的最多的是最大池化层,这种方法用一个预先取定大小和步长的池化核遍历图片,将每种遍历情况下的最大值构建新的张量值,直到遍历完成。
池化的优点是可以简化网络计算,避免过拟合风险。
3.4 Flatten Layer展平层
在模型输出之前,我们需要将张量展平,以便使用Softmax function进行激活并输出预测结果。
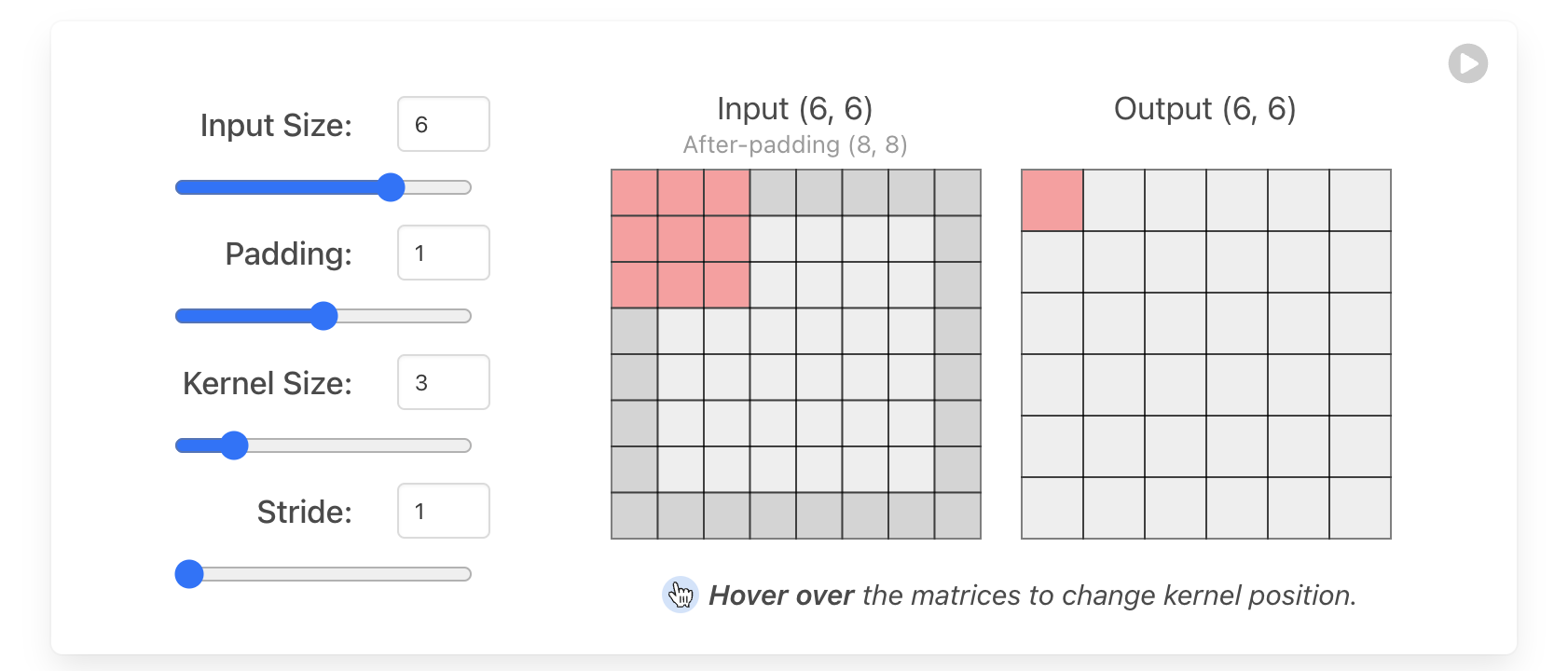
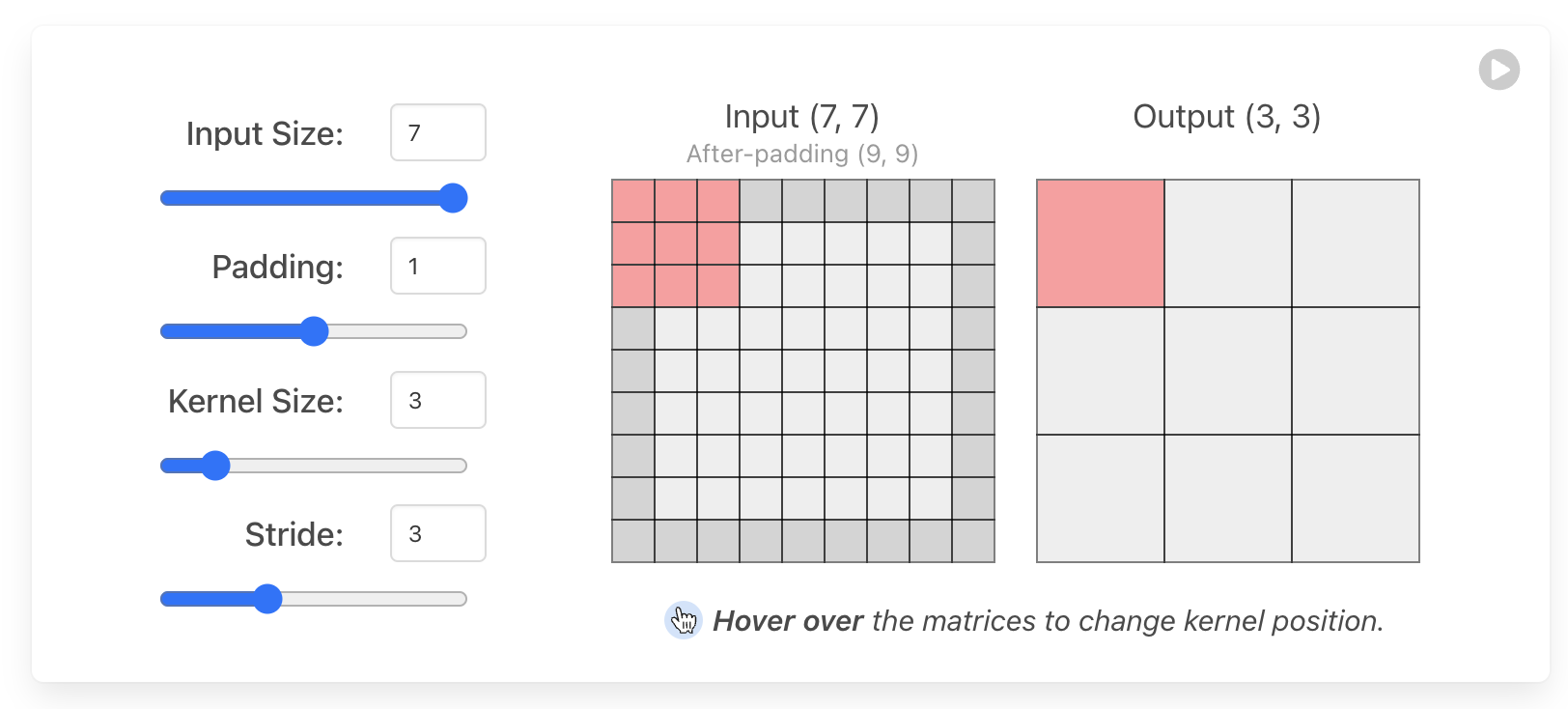
4 超参数解析
假设我们用VALID模式进行卷积,有对应关系F(input_size, padding, kernel_size, stride)
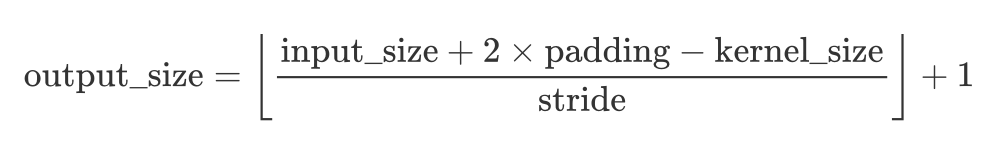
5 激活函数
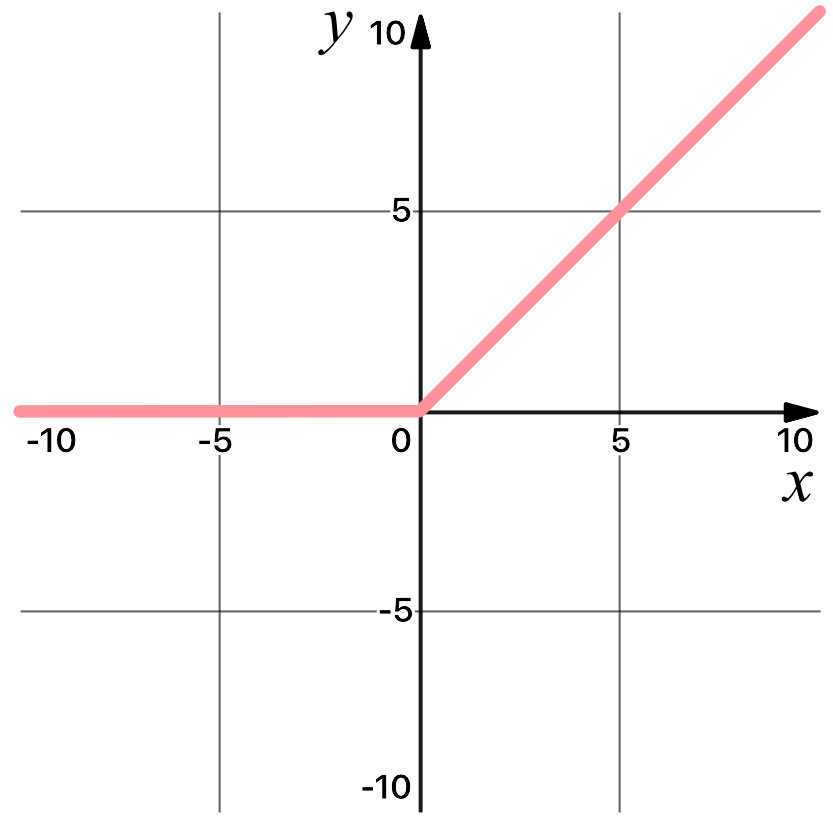
5.1 RELU
RELU函数是典型的非线性激活函数,对于神经网络来说非常重要,神经网络之所以能够实现这么高的精度,很大一部分原因就是能够表达非线性关系,而RELU函数就是很好的表达。
5.2 Softmax
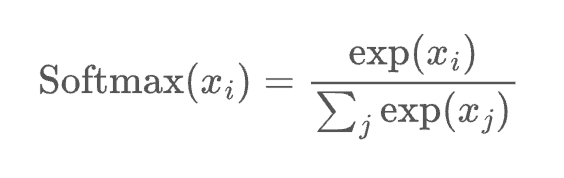
Softmax函数非常适合用来作为输出层,因为其所有分量之和加起来是1,这就与概率天然挂钩了,而且由于其指数的特性,能够放大不同值之间的差异,从而更好地实现分类。
对于不同激活函数的介绍和差异,之前学吴恩达老师的课程的时候我写了一篇笔记,请参看:https://tj-jiaoao.github.io/2023/04/26/Activate_function/






