机器学习之模型的评估与优化
当已经用现有机器学习算法(神经网络、决策树、逻辑回归等)构建了一个机器学习模型,但是模型的效果不是那么好,或者说我们想进一步优化这个模型时,我们可以怎么做呢?
比如我们的损失函数:
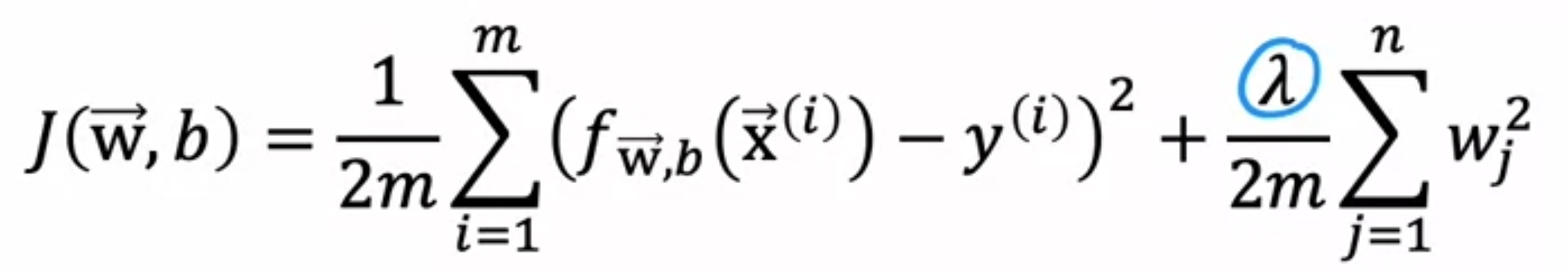
其中$\lambda$是正则化系数,我们可以尝试这些方法:
- 扩大训练样本
- 缩小特征变量维数
- 增加特征变量维数
- 增加拟合模型阶数
- 增大正则化系数
- 减小正则化系数
但是什么时候用什么方法呢?我们首先学习如何评估一个模型。
不管是回归问题还是分类问题,我们都有一个损失函数$J(\vec{w},b)$。我们要做的是最小化这个损失函数。我们通常将数据分割成 训练集和测试集两部分,通常是7:3的比例。然后分别在训练集和测试集上分别计算损失函数,如果两者最后都很小,那么可以说这个模型是有效的。(如果不是很离谱的模型,训练集上的误差大概率最后都比较小,重点看的是测试集的误差,the loss of the test data is a better indicator)
为什么需要测试集?
第一是我们需要知道模型面对未知数据的能力,不能只拿训练集的误差来衡量模型好坏,因为这些数据是用来训练的,是与调优的模型相关的数据,是“已经见过的数据”,这就好比女朋友提问她好不好看,如果要追求最客观公正的答案,那么就不能由男朋友来回答,而是要找很多路人来回答。
还有一点就是防止模型过拟合,模型可能学会了训练数据的噪声,而没有学到数据的真实分布,表现在误差上就是训练集误差非常小,这时我们可以通过看测试集误差来检查是否有过拟合的现象。
对于分类问题,除了传统意义上的损失函数计算方法外(比如逻辑回归的熵计算法),还可以用训练集和测试集中错误分类的比例来反映模型的效果。
为什么不能直接拿测试集中的数据去进行模型选择?
测试集的目的是检验模型面对未知的新数据的能力,如果用测试集数据干预了模型选择的过程,那么测试集中的数据就会被“污染”。换句话说,这种行为就是在询问亲近的兄弟:我女朋友美不美,也得不出客观的评价。
最终解决方案:训练集 + 交叉验证集 + 测试集(6:2:2)
其中训练集用来训练模型参数,交叉验证集用来衡量模型性能,用于模型选择,测试集用来测试模型对未知数据的预测能力。流程如下:
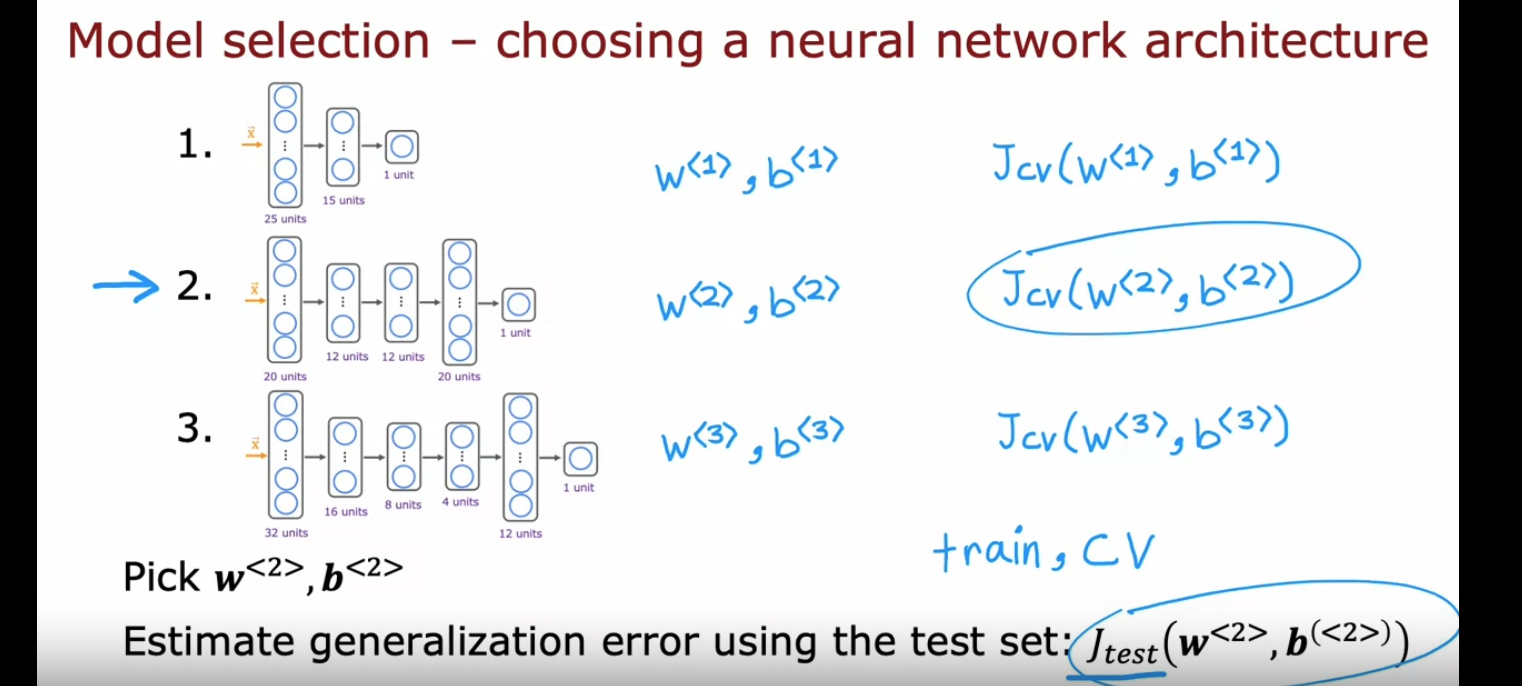
但是假设有这样一种情况:这个模型相比其他模型好一些,但是在训练集和测试集上的误差都比较大,表现都不尽如人意,我们应该如何调整模型呢?
我们先来了解一下两种极端的现象:高偏差(High bias)和高差异(High variance)
- 如果$J(train)$和$J(cv)$都比较高,那么模型表现为High bias
- 如果$J(train)$比较低,但$J(cv)$很高,那么模型表现为High variance
- 还有一种情况可能既High bias 又 High variance,一般会在神经网络中出现,但这种现象并不常见

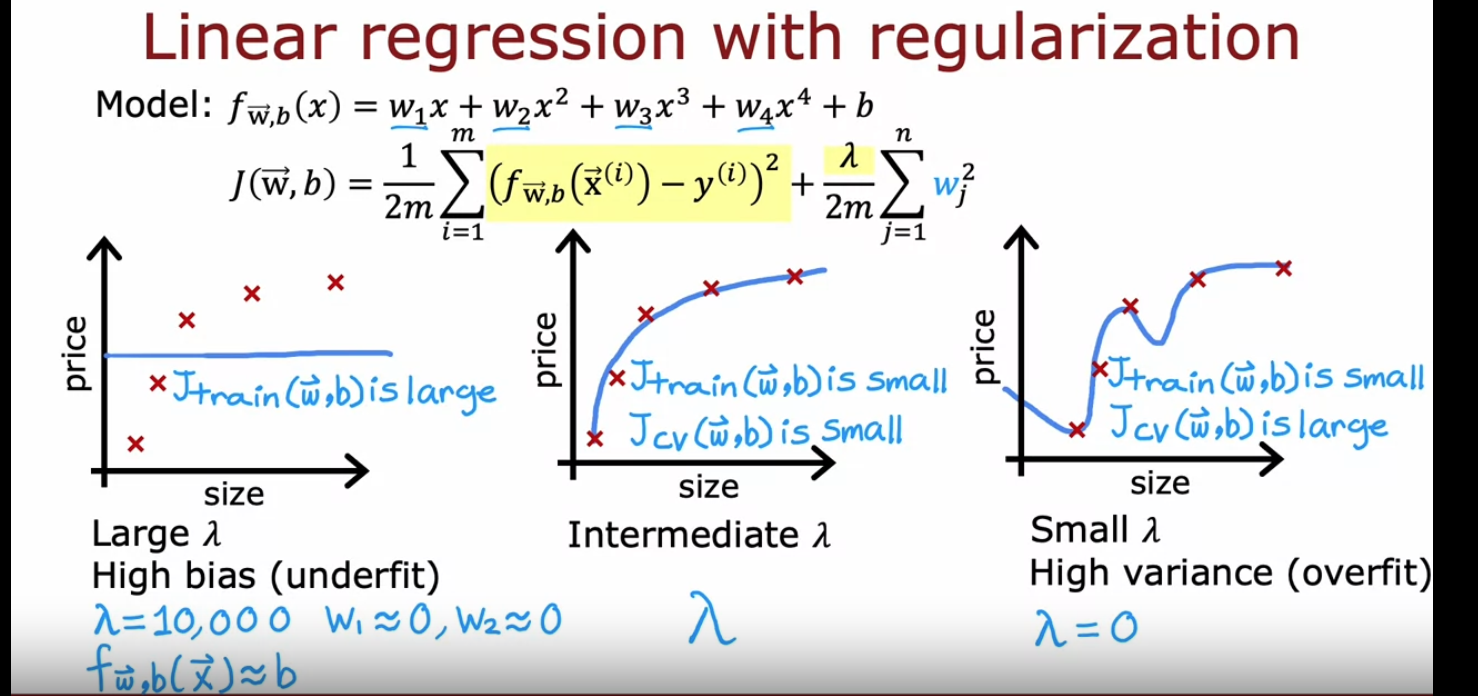
多项式系数和正则化系数都可以影响模型的偏差和差异,具体曲线如下图:
回忆:正则化是通过引入惩罚系数$\lambda$来调整模型的高次项参数,从而一定程度上解决过拟合的问题,因为如果惩罚系数比较大的话,高次项系数就会比较小,模型的“弯曲程度”就会减小,过拟合的风险就会降低。
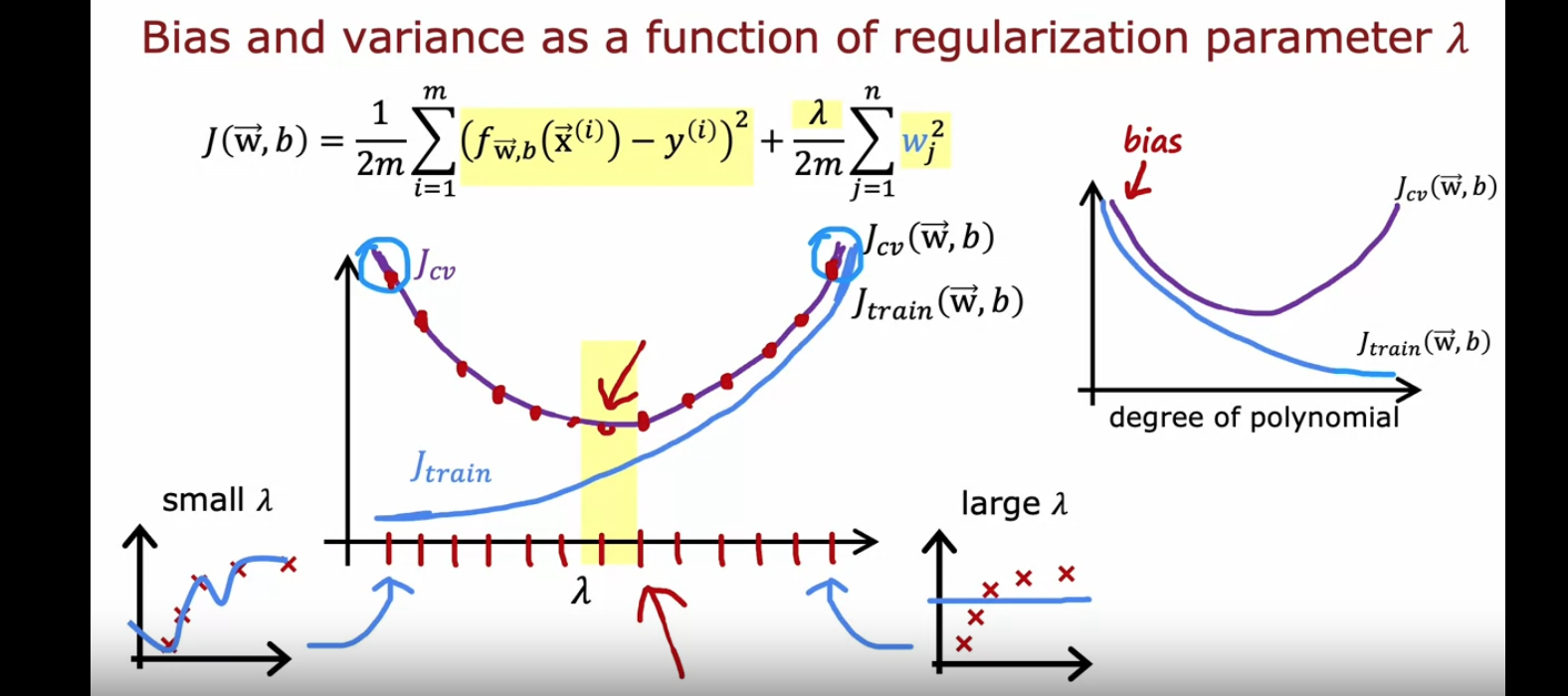
那么什么样的$J(train)$和$J(cv)$可以被称为“大”呢?
我们需要找一个基准(baseline)去了解这个问题,通过对比baseline和$J(train)$,我们可以判断是不是High bias;通过对比$J(train)和$$J(cv)$我们可以判断是不是High viriance.

我现在想知道,增大训练样本数量对提升模型效果有没有用,这就引出了“学习曲线”的概念。学习曲线是$J(train)$和$J(cv)$随着训练样本数的增大而改变的曲线,一般来说长这样:
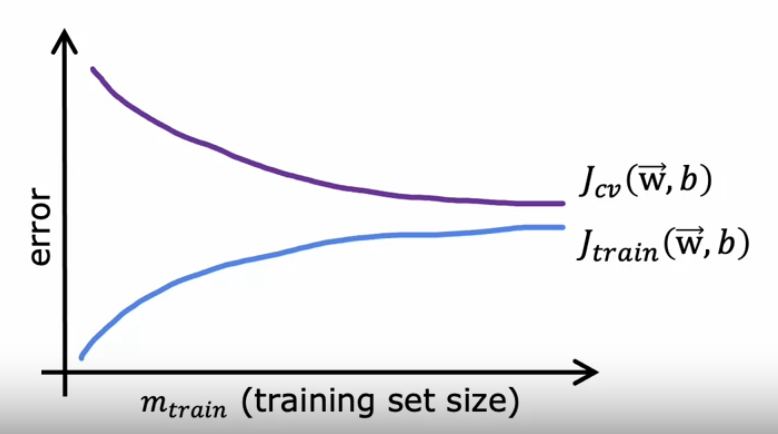
当训练样本数量很小时,因为模型没有足够的数据学习到真实的分布,所以$J(cv)$很高,但是模型很好地拟合了所给的数据,所以$J(train)$比较低。
当样本的数量不断增大时,这是模型慢慢很好地学习了模型的真实分布,$J(cv)$不断减小,但是由于数据的真实分布越来越难用当前模型拟合,所以每增加一个训练数据,其实就给$J(train)$引入了新的误差,所以$J(train)$在不断增大。
我们说比较$J(train)$和baseline可以看出模型是否高偏差。比较$J(train)$和$J(cv)$可以看出模型是否过拟合。从这张图可以看出模型是否过拟合,如果训练的$J(train)$和$J(cv)$相差比较大,那么模型就有过拟合的问题,这时候通过增加训练样本数量可以解决过拟合问题,让模型更好地学习真实的数据分布。
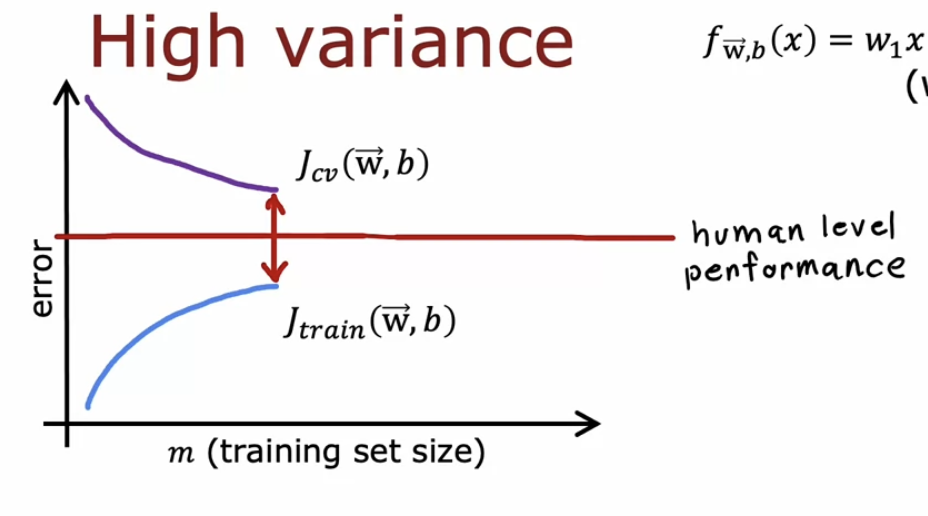
但是如果$J(train)$比baseline大很多的话,就属于高偏差的问题,这时候通过增大样本数量就不会起什么作用了。这时候就需要更换模型来解决问题了?
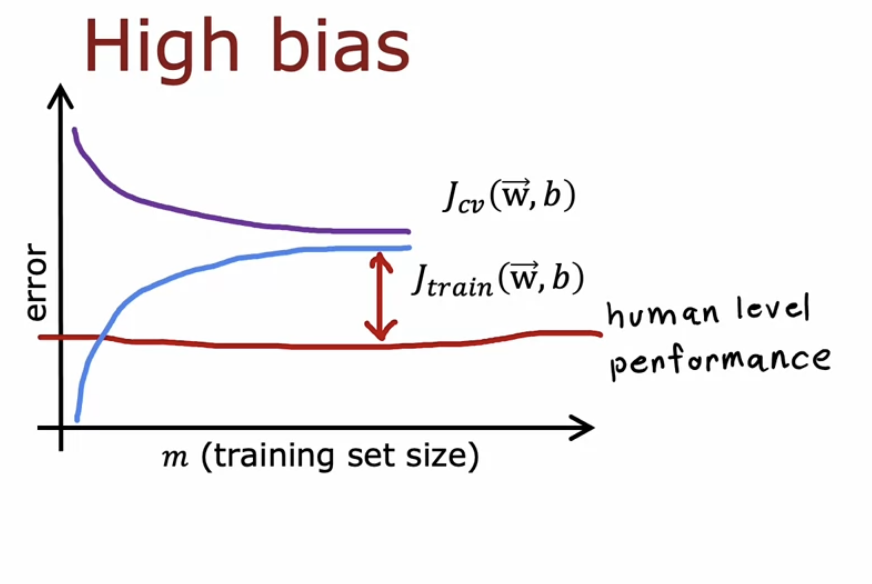
现在,我们可以通过识别是High bias或者High variance来挑选上述6种方法对模型进行调整了。
- 扩大训练样本 – 针对High variance
- 缩小特征变量维数 – 针对High variance
- 增加特征变量维数 – 针对High bias
- 增加拟合模型阶数. – 针对High bias
- 增大正则化系数 – 针对High variance
- 减小正则化系数 – 针对High bias
对于神经网络来说,上面的理论仍然适用,并且神经网络的优点之一就是可以作为一个很好的方式解决High bias和High variance。基本流程如下:
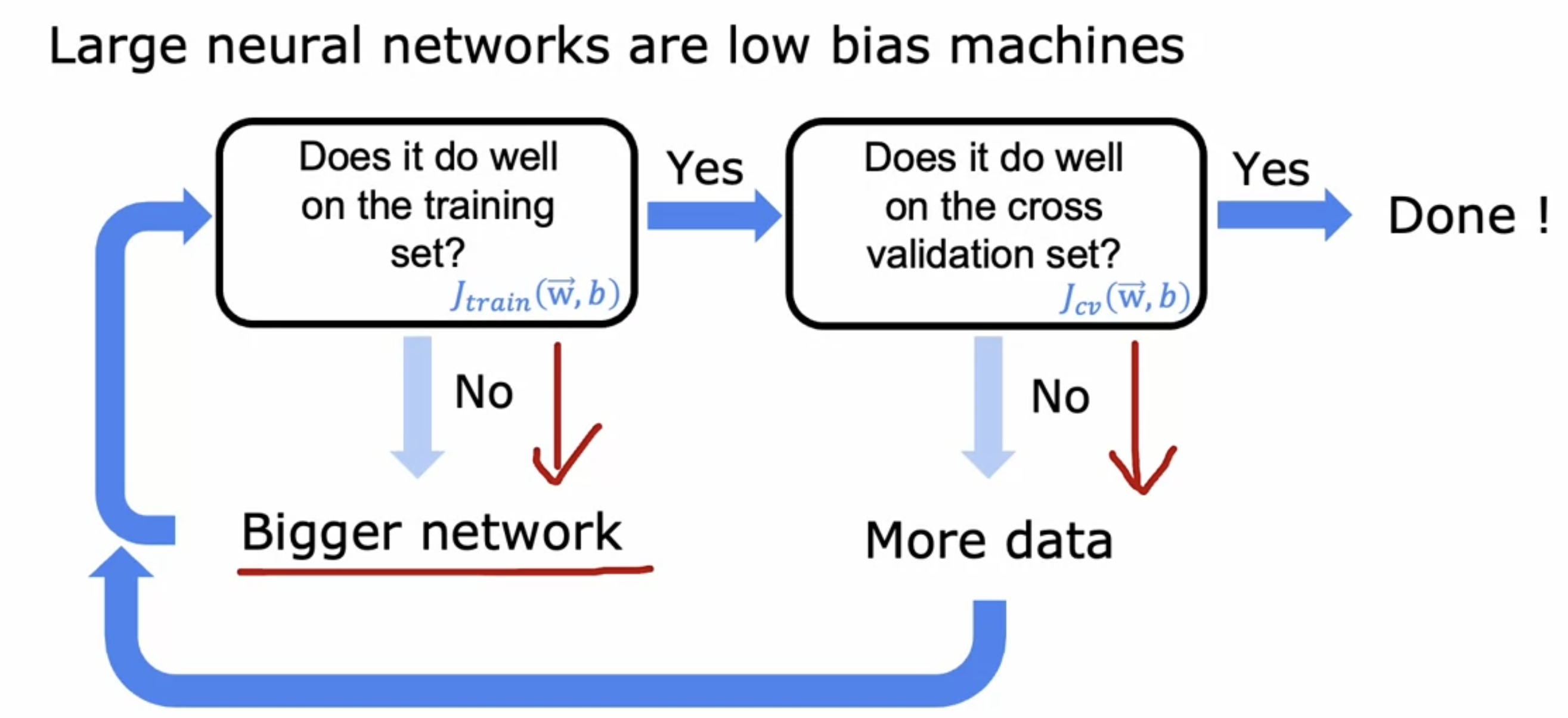
首先看模型是不是High bias,如果是的话就增大网络复杂度,可以增加隐藏层或者增大每一层的神经元数,直到模型表现良好(和baseline相比),然后需要检查$J(cv)$,如果$J(cv)$太大的话需要扩大样本数量,然后需要重新判断模型是不是高偏差,如此循环往复,直到High bias和High variance都解决为止。
当然,正则化在神经网络中的作用也是很大的。事实表明,只要正确地选取正则化系数,复杂的神经网络架构+正则化总是比简单神经网络表现出色,缺点就是复杂的神经网络消耗算力较大,硬件成本较大。
拓展知识:迁移学习
迁移学习指的是用已经训练好的模型参数来训练相似的任务。它包括两个步骤:
- supervised pretraining 迁移预训练。首先在一个大数据集上训练一个任务,获得其最终的模型参数
- Fine-tuning。 然后使用训练好的模型参数作为初始参数来训练另一个任务。这里有两种方法,第一种是只训练最后一层的参数,这个适合当前只有小数据集,第二种方法是把模型参数全部再训练一遍,这种方法适合有相对较大的数据集。不管哪种方法,训练的效率都比从0开始训练快得多。
‼️能够进行迁移学习的重要依据是任务之间共享表示,比方说图像识别任务,都需要识别图片的形状、边缘、纹理等特征。如果任务之间没有足够的相似性,迁移学习并不能提高性能。
拓展知识:精确率(precision)和召回率 (recall)
先来看混淆矩阵:
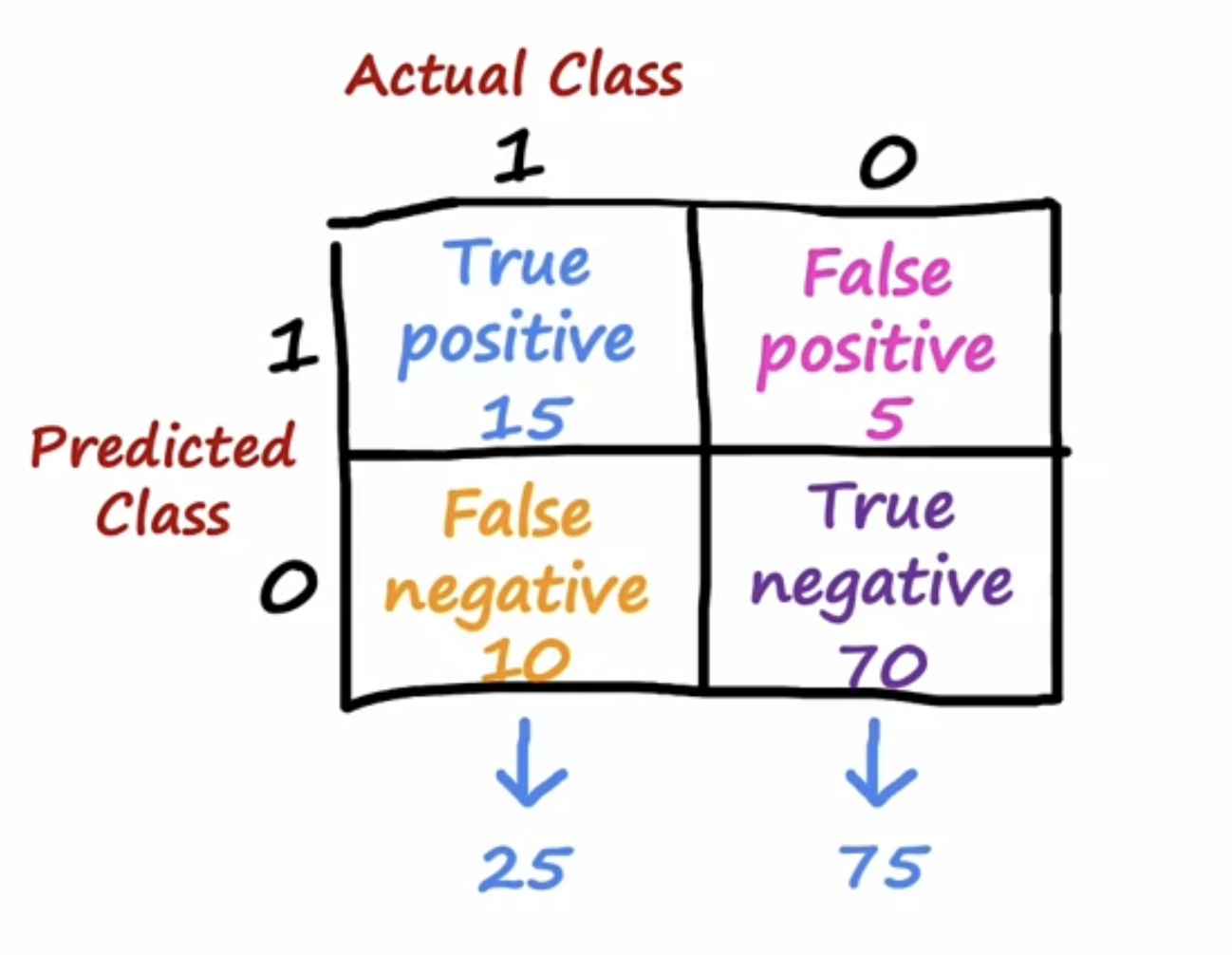
精确率precision:实际和预测同时为正例 / 预测值全部为正例
召回率recall:实际和预测同时为正例 / 实际值全部为正例
精确率和召回率是一对矛盾的量,一个高的话,另一个必定低,关系图如下:
把threshould调高之后,找出来的正例是真正的正例的概率提高了,但是漏网之鱼变多了,就是说真正是正例,但是没找出来,总结来说就是“找到了,但没完全找到”。用捕鱼的例子,网的孔隙变大了,有些鱼就抓不到了。
把threshould调低之后,真正的正例就更容易被识别出来了,但是因为判断正例的标准变低了,所以很多真实的负例也会被筛选出来判断为正例,总结来说就是“宁可错杀一千,也不放过一人”。用捕鱼的例子,就是孔隙变小了,一些小鱼小虾也会被捞上来了,但是捞上来的肯定有我们想要的鱼。
那么如何确定孔隙大小呢?精确率和召回率之间的平衡点,一般是使用F1系数表示。这种加分之乘形式的函数很适合用来表征有反相关关系的两个变量之间的最优化问题,只要最大化这个函数的值就可以找到一个令两个变量都高的一个平衡点。





