两两交换链表元素

题目描述

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

24.两两交换链表中的节点-题意

思路解析

两两交换节点必然涉及多指针操作，需要更改多个节点的next指向，并且交换是两两的，由此我想到了用双指针的方法。通过一前一后两个指针，分别指向每次交换的节点的方法来更新链表。

![[Pasted image 20230828234204.png]]

上图是一般的更新思路，但是这种方法细想，其实有很多问题。

  1. 按照上图的更新方式，对于1节点来说，bp->next = fp->next->next。但是当节点3，4不存在或4不存在的时候，这样的更新方式就会出错
  2. fp和bp的更新可以通过临时节点来实现，但是还是会存在上述的问题，如何能保证不会空指针异常需要耐心调试
  3. 循环何时结束是需要考虑的一大问题

想必读者也看出上述方式的复杂性了，因为我们没能找到一个统一的更新思想，所以当边界条件很多时避免不了分类讨论，操作会很繁琐。

不过调试就调试呗，以下是这种实现方式的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ListNode* swapPairs(ListNode* head) {
        if (!head || !head->next)   return head;
        ListNode* hn = new ListNode(0, head->next); // 头节点，方便返回
        ListNode* fp = head->next;
        ListNode* tp;
        ListNode* bp = head;
        while(fp){
            tp = fp->next;
            bp->next = tp?(tp->next?tp->next:tp):nullptr; // 分类更新，共三种情况。
            fp->next = bp;
            bp = tp;
            fp = bp?bp->next:nullptr;
        }
        return hn->next;
    }

上述代码中bp的更新是最难的，不过其实只有三种情况：

  1. 当前bp-fp对之后没有下一对了，此时更新为nullptr
  2. 当前bp-fp对之后只有单身狗了，此时更新为tp
  3. 当前bp-fp对之后还是一对，此时更新为tp->next

此外fp也要根据bp的情况进行更新。

读者想必要问，有没有相对统一的，不用这样分类讨论的方法？
Carl哥给我们的方法就是相对统一的，还是上面的例子,不过我们加上头节点和一个cur指针：
![[Pasted image 20230828235922.png]]

这种方法的核心思想是：通过让cur指向需要改变的节点对的前一个节点来实现更换操作.为什么要指向前一个节点呢？如果按照我们刚刚的思想，指针指向第一个节点不行吗？

如果指向第一个节点，那么后面一个节点对的情况就势必会影响到这个节点对，由此带来分类讨论的问题。如果指向前一个节点，那么我们就可以找出一个更新规律：

最后，每次更新完链表之后还需要将cur指向下一对节点的前一个节点，上述实例中是1节点。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ListNode* swapPairs(ListNode* head) {
        ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向head，这样方面后面做删除操作
        ListNode* cur = dummyHead;
        while(cur->next != nullptr && cur->next->next != nullptr) {
            ListNode* tmp = cur->next; // 记录临时节点
            ListNode* tmp1 = cur->next->next->next; // 记录临时节点

            cur->next = cur->next->next;    // 步骤一
            cur->next->next = tmp;          // 步骤二
            cur->next->next->next = tmp1;   // 步骤三

            cur = cur->next->next; // cur移动两位，准备下一轮交换
        }
        return dummyHead->next;
    }

删除链表的倒数第n个节点

本题只需要想到使用区间双指针就会很快，如果不用虚拟头节点的话需要加上对头节点删除的条件判断，总体来说不难。

1
2
3
4
5
6
7
8
9
10
11
12
ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* fp = head, *bp = head;
        
        for (int i = 0; i < n; i++,fp=fp->next);
        if (!fp)    head = head->next;
        else 
        {
            for(;fp->next;fp=fp->next,bp=bp->next);
            bp->next = bp->next->next;
        }
        return head;
    }

链表相交

题目描述

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

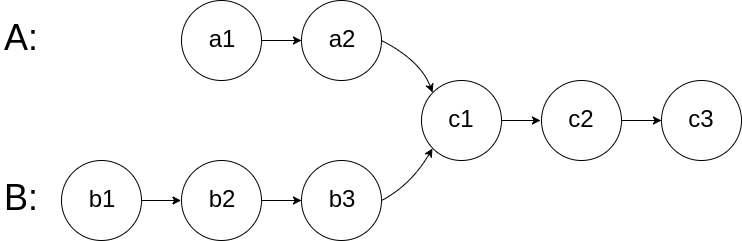
题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

思路解析

首先求出两个链表的长度，然后用对齐的双指针逐一推进即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int len(ListNode* n){
        int sz = 0;
        for (sz; n;n=n->next,sz++);
        return sz;
    }

    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        int szA = len(headA), szB = len(headB);
        ListNode* pa = headA, *pb = headB;
        unsigned int offs = szA - szB > 0?szA - szB:szB-szA;
        if (szA < szB)
            for (int i = 0; i < offs; i++)  pb=pb->next;
        else    
            for (int i = 0; i < offs; i++)  pa=pa->next;
        for(;pa && pb; pa=pa->next,pb=pb->next){
            if (pa == pb)   return pa;
        }
        return nullptr;
    }

环形链表

题目描述

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

1
2
3
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

题目解析

既然是环形链表，就可以用环形链表的数学性质来解决。我们从头节点开始一直前进，会在环的入口处进入循环，不断地“绕圈”。如果我们设置双指针，一快一慢，两指针一定会在循环中相遇。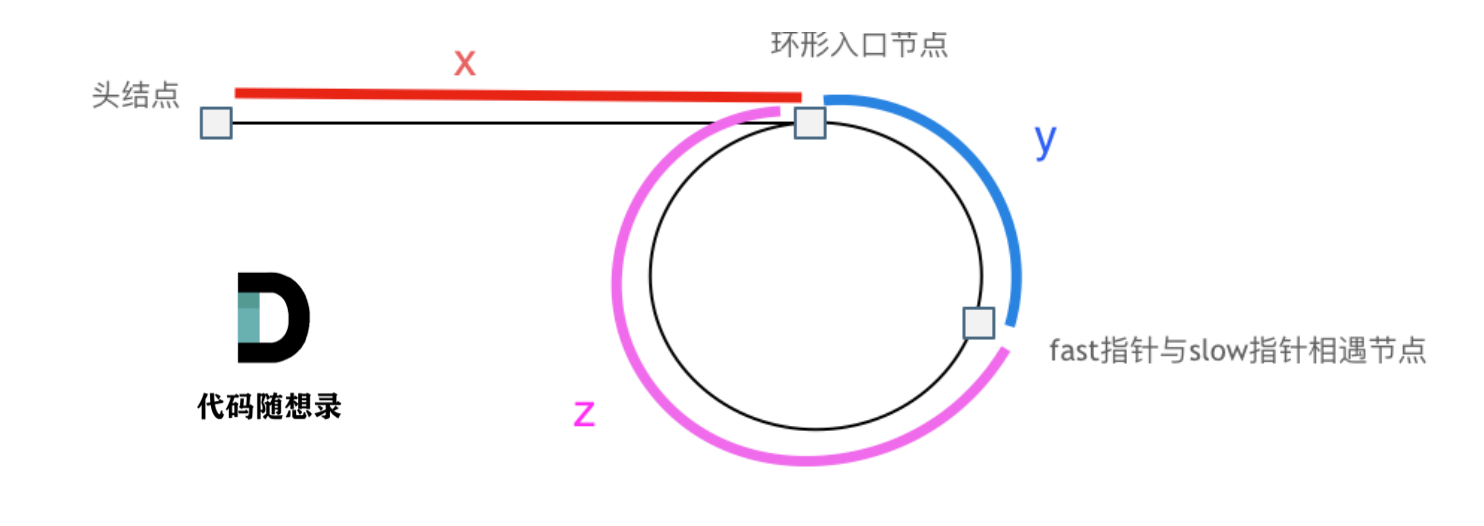

设相遇时慢指针经过了$x + y$个节点，那么快指针经过了$x+n(y+z)+y$个节点，这里的n表示快指针经历的循环数。这是个追击问题，因为快指针每次走两步，慢指针每次走一步，所以有：

$$
\frac{x+y}{1} = \frac{x + n(y+z)+y}{2}
$$

整理得：

$$
x = (n-1)(y+z) + z, n>= 1
$$
从这个公式可以看出，所求的x就等于一个指针从相遇节点出发，转(n-1)圈然后再走z步。所以我们再设置两个指针，一个从头出发，一个从相遇节点出发，每次都走一步，相遇的地方就是所求环的入口。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ListNode *detectCycle(ListNode *head) {
        ListNode* fp = head, *sp = head;
        while(fp&&fp->next){
            fp = fp->next->next;
            sp = sp->next;
            if(sp == fp){
                ListNode* tp1 = head;
                ListNode* tp2 = fp;
                while(tp1!=tp2){
                    tp1 = tp1->next;
                    tp2 = tp2->next;
                }
                return tp1;
            }
        }
        return nullptr;
    }