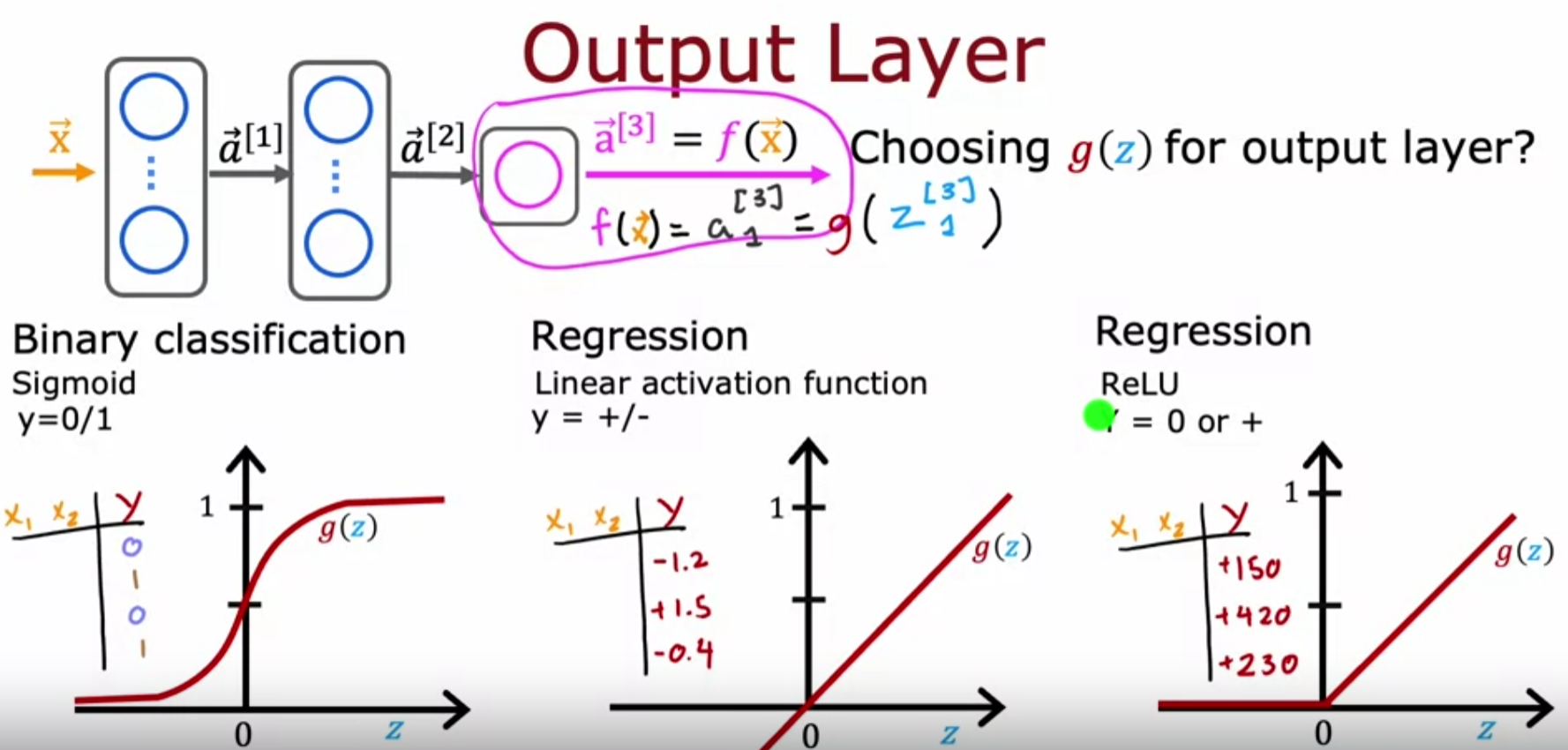
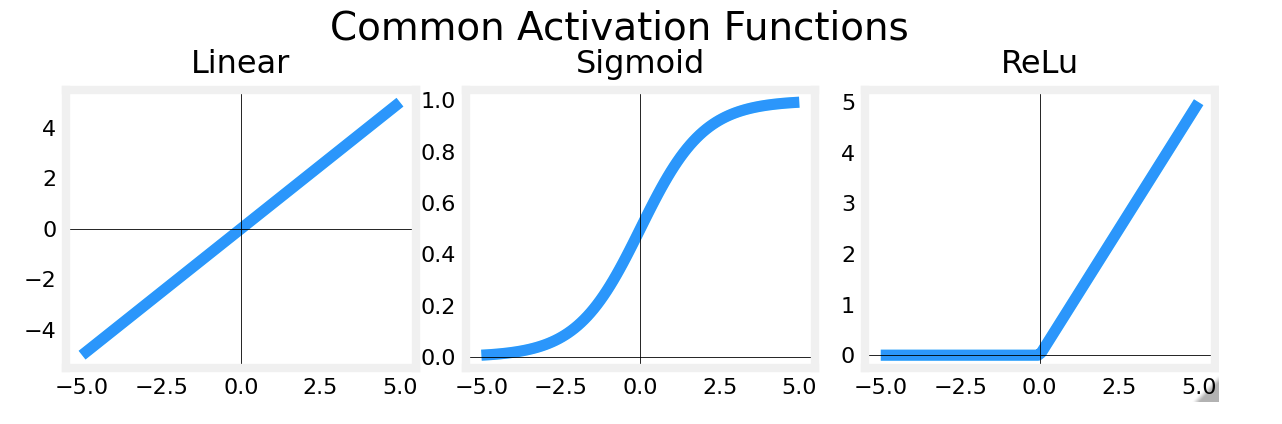
Untitled

输出层

Untitled

  • 当输出是0/1值时采取Sigmoid Function
  • 当输出是连续值，并且能取正负值时选取线性激活函数（也就是没有激活函数）
  • 当输出是非负值时取ReLU激活函数：g(z) = max(0,z)

隐藏层

隐藏层中最广泛使用的是**ReLU函数**，对比Sigmoid函数的原因如下：

  • 计算ReLU函数比Sigmoid函数快很多
  • 计算梯度下降时速度和图像的斜率有关，因为sigmoid函数在图像两边的斜率太小，梯度要迭代很多次才能收敛。而RELU不会出现这个问题

代码

1
2
3
4
5
6
7
from tf.keras.layers import Dense

model = Sequential([
	Dense(units = 25, activation = 'relu'), # layer1
	Dense(units = 15, activation = 'relu'), # layer2
	Dense(units = 1, activation = 'sigmoid') # output layer
])

其他

  1. 还有另外一些激活函数如tanh(双曲正切函数）, LeakyRELU, swish ,不过上述三个激活函数已经足以适用于大部分模型了
  2. 为什么要搞这些花里胡哨的激活函数，直接输出不好吗？就将一个模型的输出当作另一个模型的输入就好了呀？（激活函数的意义）

Untitled

可以看到如果隐藏层和输出层都用线性回归，那么本质还是线性回归，神经网络完全没有发挥作用。

如果隐藏层全是线性激活函数，输出层是sigmoid激活函数：

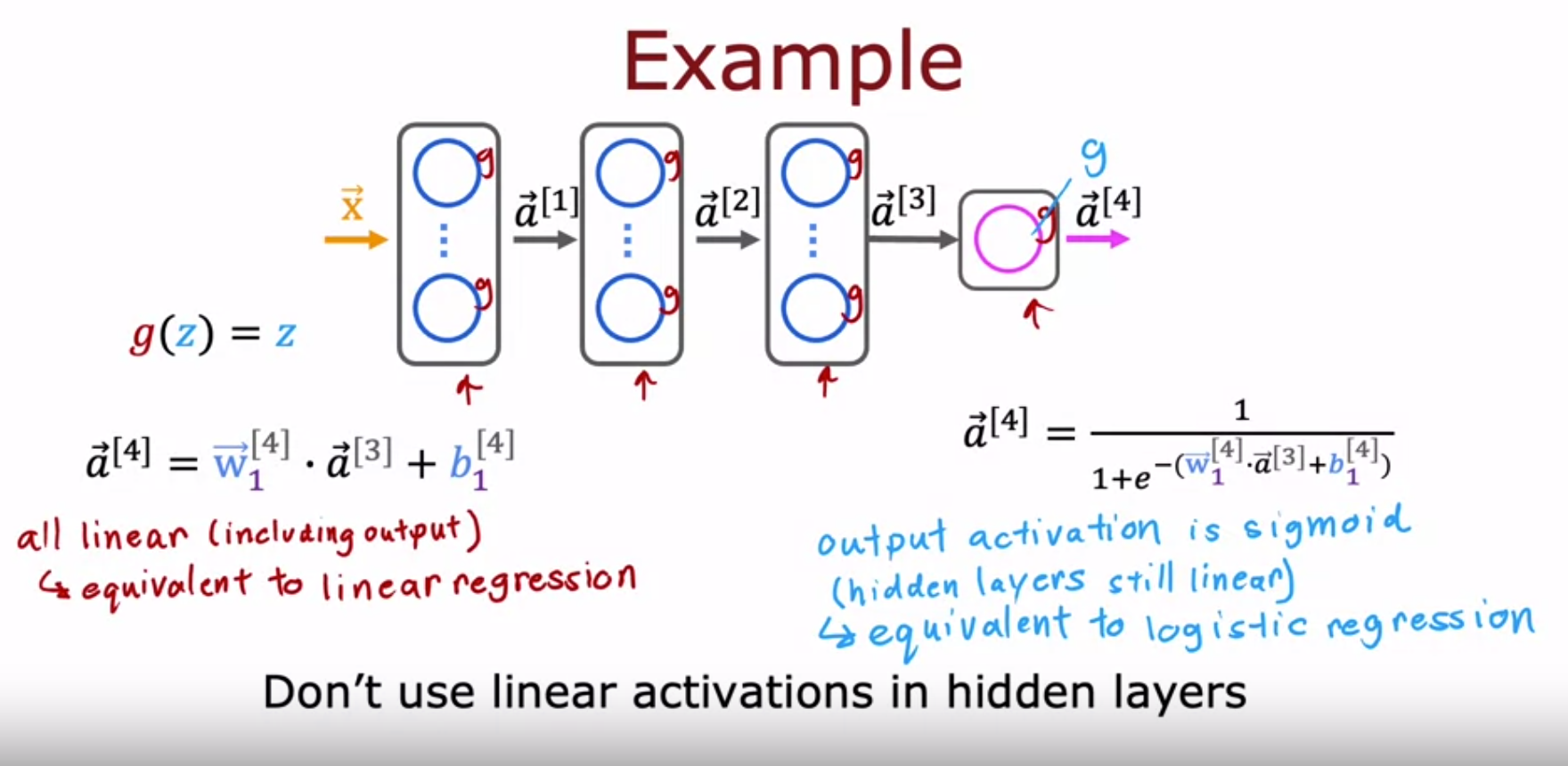
Untitled

那么这么多隐藏层其实就只做了一个线性回归，然后在输出层做了一个逻辑回归。所以这个神经网络和逻辑回归做的事情其实是一样的，并没有任何优化。所以普遍的规则是不要在隐藏层中使用线性激活函数（Q：那ReLU不是也只是把负数部分变为0了嘛？正数部分还是不变的呀？这样的非线性变换就可以说适合用作隐藏层的激活函数了？当输入变量全都是非负值那效果不还和线性激活函数一样的嘛？）

A: ReLU是通过wx + b的正负情况来控制是否让这部分unit输出发挥作用，从而达到不同unit负责不同的输入部分的目的（详情见下）

  1. 用非线性的激活函数的作用：

Untitled

就是说输入很有可能是分段的，在每个转折点会有一个新的线性函数，比方说一条曲线分为三段，现在对其用神经网络做回归预测分析，第一层有三个units,ReLU函数可以使只有unit 0负责第一段的预测，就是说unit2和unit3经过w和b的调参可以使得当输入x位于第一段时，unit2和unit3算出来的z是负数，所以激活为0，这样就达到了不同unit控制不同输入段的作用，神经网络的特性就体现出来了。

ReLU(Rectified Linear Unit)

1
𝑎=𝑚𝑎𝑥(0,𝑧)      # ReLU function

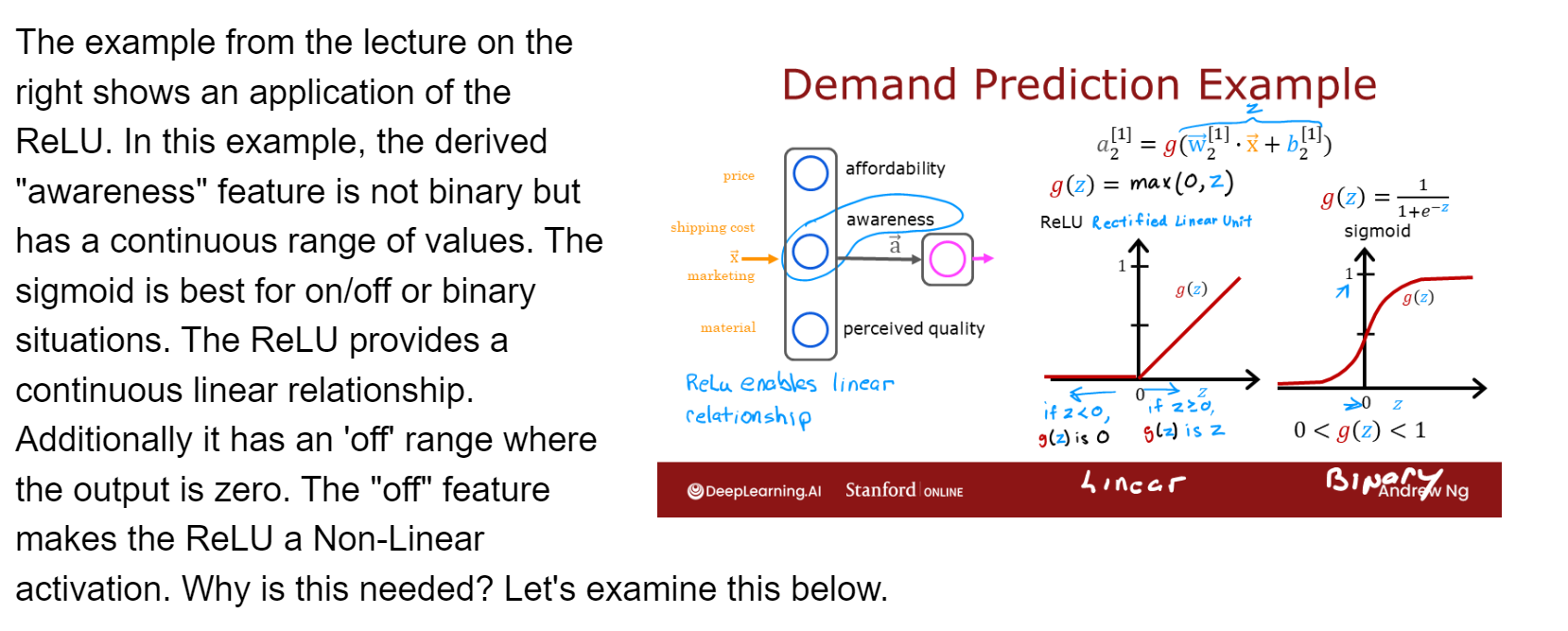
Untitled

The “off” or disable feature of the ReLU activation enables models to stitch together linear segments to model complex non-linear functions.

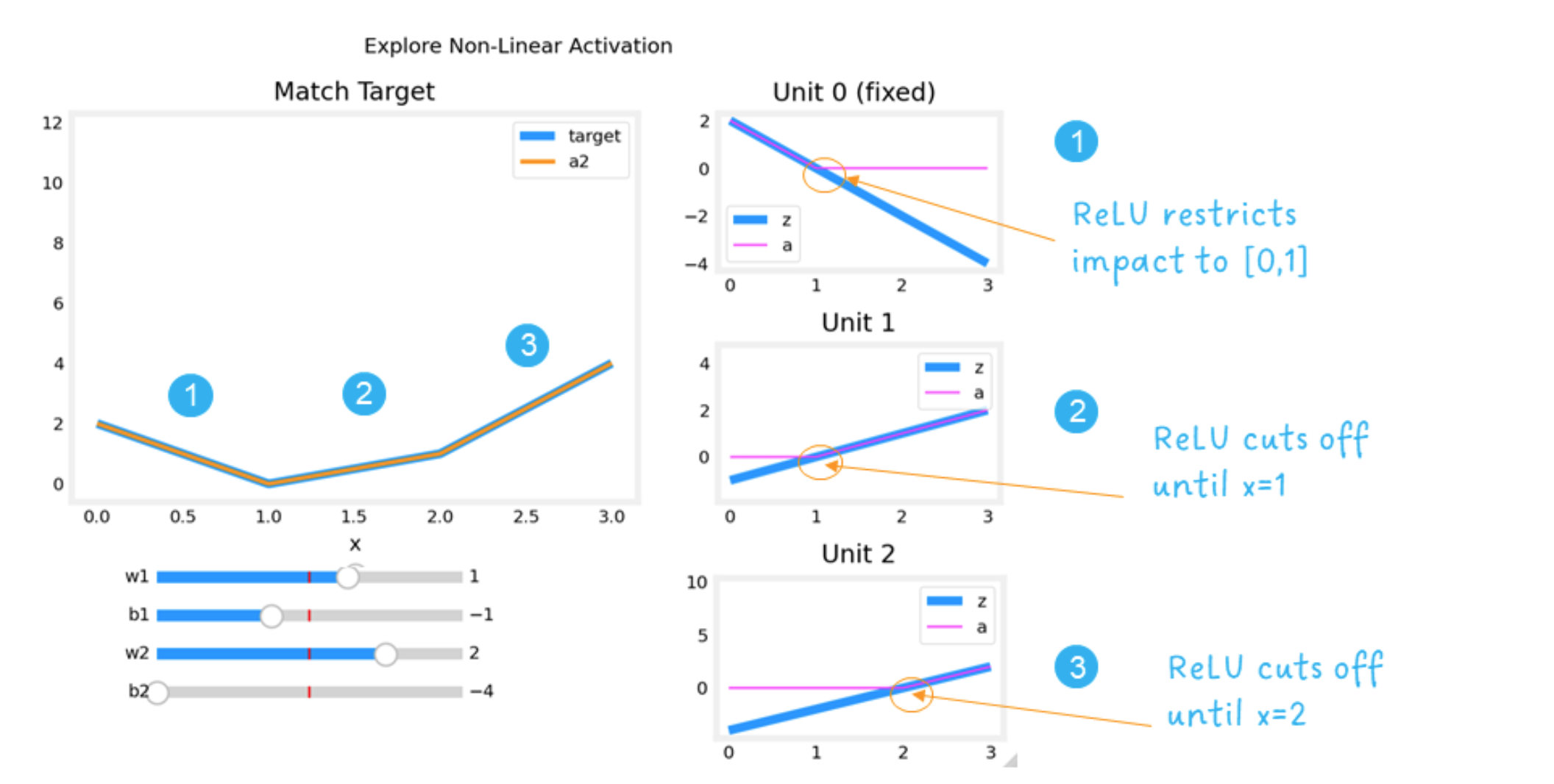
Untitled

Untitled

因为对于已经预设好的unit0，由于ReLU函数的限制，只有当x0处于(0,1]之间时输出才不是0，所以unit0控制的就是曲线在(0,1]之间的输出；我们不想让unit1 和 unit3 控制[0,1]的预测，所以通过调整w1,b1,w2,b2可以实现当x > 1时unit1开始控制，当x > 2 时unit2开始控制。

综上，ReLU激活函数就是这样进行非线性的复杂规律的预测的